research

My research focuses on developing hybrid quantum algorithms based on physical insight leveraging quantum and classical resources. Those developments are realized within automatized software frameworks so that other researchers can apply, extend, and integrate them into their works.

Here are three examples focusing on different aspects of variational ground state optimization :

  1. qubits: JCPL 2021 (arxiv:2008.02819)
  2. circuits: PRA 2022 (arxiv:2105.03836)
  3. gradients: Chemical Science (arxiv:2011.05938)

through the tequila library all three developments are automatically available to interested partys

import tequila tq

mol = tq.Molecule(geometry="beh2.xyz") # uses 1

U = mol.make_ansatz("SPA")             # uses 2
H = mol.make.hamiltonian()
E = tq.ExpectationValue(H=H, U=U)

result = tq.minimize(E)                # uses 3

Scientific Computing & Software



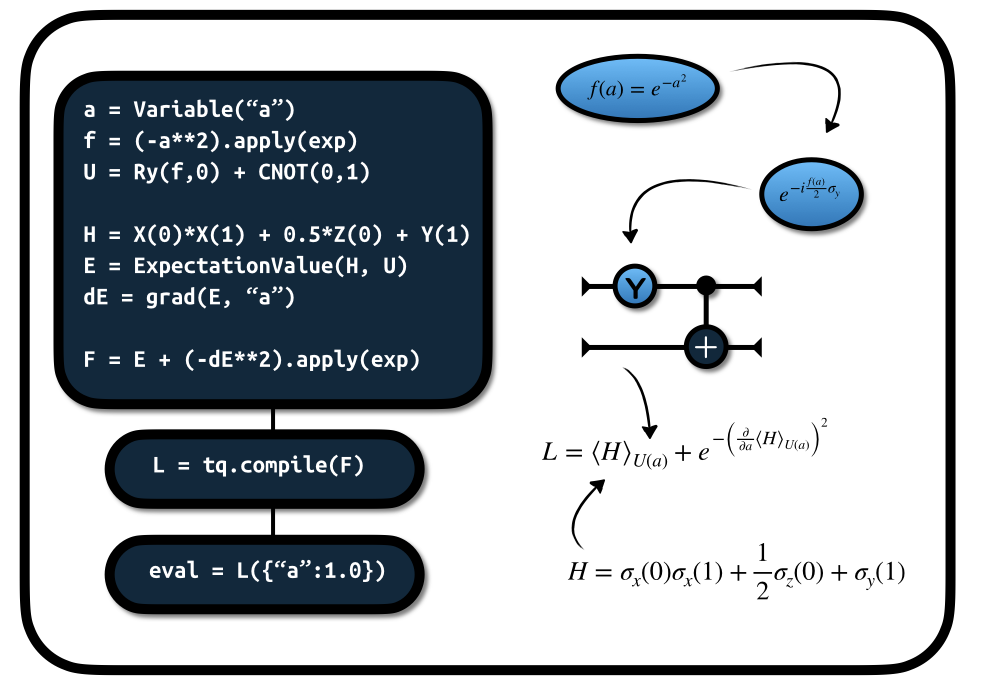
With high hopes for a powerful future impact on various scientific and industrial applications, the ecosystem of quantum algorithms is proliferating. In the current stage, the field is maturing to a point where it becomes essential to demonstrate new ideas explicitly on actual use cases. The problems often become too complicated for pure theoretical estimates. In addition, one usually deals with a multitude of connected algorithmic procedures and heuristics, rendering manual engineering unfeasible. At this stage, automatized frameworks are crucial to advance further.

Representative publications:

Blog entries:

Approximations & Intperpretability



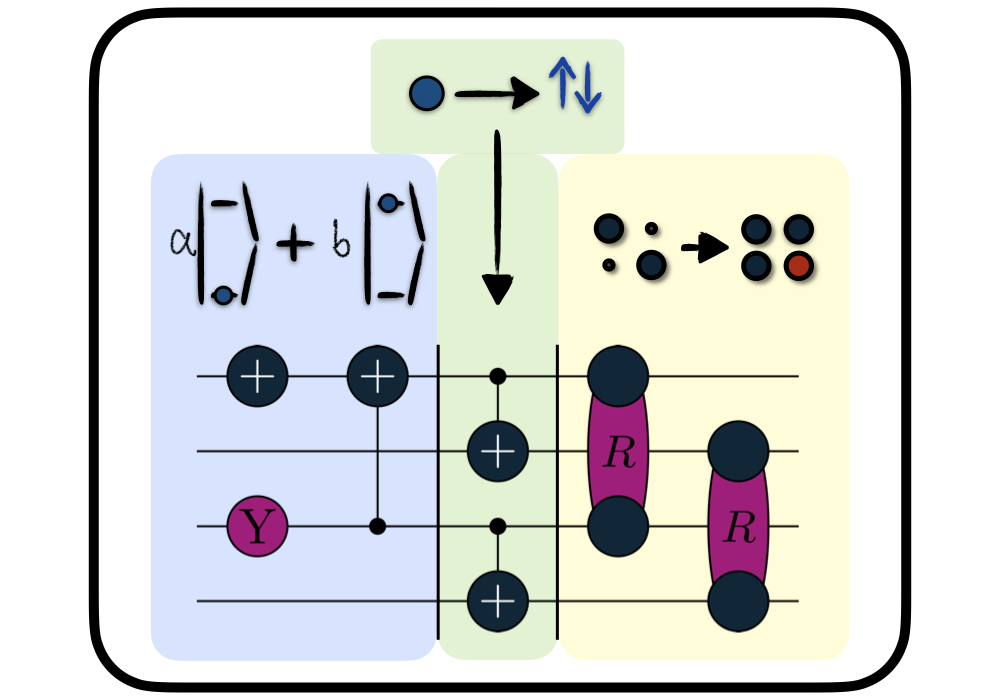
An integral part of science is the formulation of abstract concepts capable of capturing the essential aspects of complex processes to keep the concept as simple as possible. Currently, such ideas for the construction of quantum circuits are in high demand. For example, in the context of variational approaches, the design of the circuit determines which states we can reach through variational optimization. It is often the crucial element for success. Interpretable techniques allow us to construct circuits faster and predict their performance more confidently.

Representative publications:

Multiresolution Quantum Chemistry

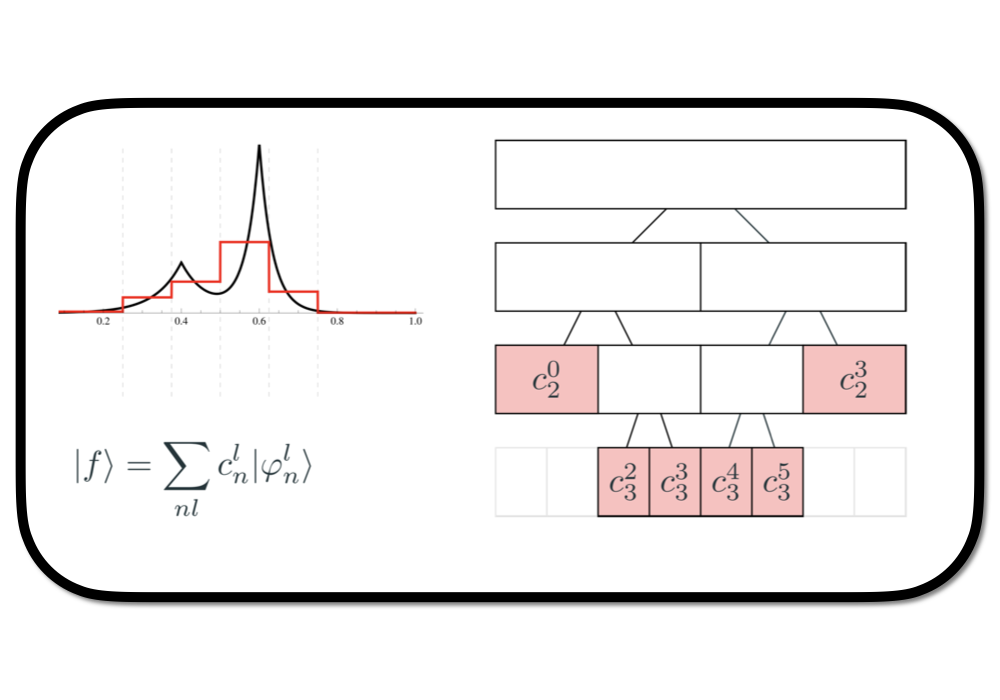
Traditional electronic structure methods are usually rigid in their numerical representation and rely upon globally pre-defined sets of Gaussian functions whose application requires substantial knowledge if we want to interpret or predict chemical reactions. Multiresolution quantum chemistry offers an alternative where the orbitals are represented by a multiresolution analysis - a recursive decomposition of the spatial one-particle Hilbert space that allows automatic adaptive construction of a scale-invariant spectral element representation. From a user perspective, we can ignore the numerical details. Astonishingly, this often also holds for the development of new applications. I use madness for implementation and integration of the developed methods.

Representative publications:

Blog entries:

Black-Box Methods



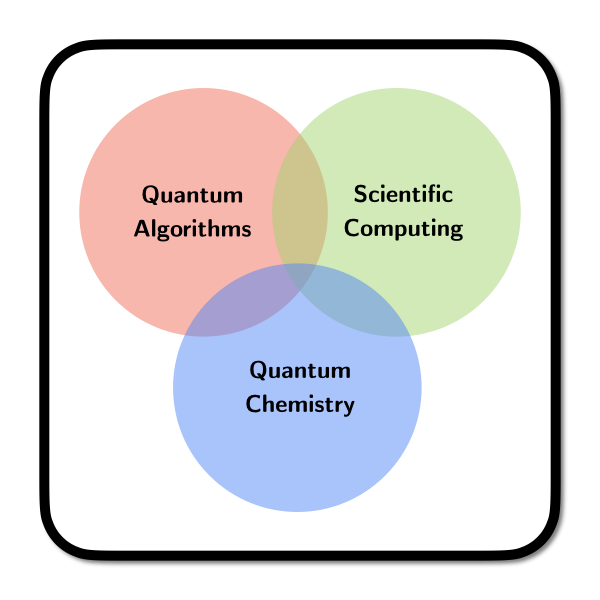
To render new numerical algorithms or heuristics applicable, it is essential to provide them within a robust and easy-to-use software framework with useful defaults for all internal parameters and thresholds. Ideally, the method can be applied as a black box - meaning the user does not need to bring any knowledge about the underlying details to use the software. In reality, we often can not provide a full black box, but for most methods we can get close. Within my research, I aim to come as close as possible to this ideal. Some developments would not have been possible without this paradigm in the first place.

Representative publications where robust black-box procedures, as illustrated in the code-box on top of this page, were crucial for the demonstration of new ideas:

  • JCPL 2021 (see above) relies on the implementation of JCP 2020 with itself relies on the automatized construction of suitable guess orbitals implemented in PCCP 2015
  • PRR 2022: Conceptual work on defining trust-intervals for variational approaches led by Maurice Weber (ETH). We applied our black-box approaches to circuit construction, gradient computation and basis-set-free orbital generation.
  • QST 2021: Work led by Zi-Jian Zhang (UofT) on prescreening of operator pools for adaptive circuit construction. We applied our black-box approaches to basis-set-free orbital generation.
  • PCCP 2022: Work led by Philipp Schleich (UofT) on energy corrections with explicit correlation. We applied our black-box approaches to circuit construction, gradient computation and basis-set-free orbital generation.